
#include "common.h"#include <stddef.h>#include <stdio.h>#include <strings.h>#include <math.h>#include "machine.h"#include "vmath.h"#include "db.h"#include "nmg.h"#include "raytrace.h"#include "rtgeom.h"#include "./debug.h"Include dependency graph for g_rhc.c:

Go to the source code of this file.
Data Structures | |
| struct | rhc_specific |
Defines | |
| #define | RHC_NORM_BODY (1) |
| #define | RHC_NORM_TOP (2) |
| #define | RHC_NORM_FRT (3) |
| #define | RHC_NORM_BACK (4) |
| #define | RT_RHC_SEG_MISS(SEG) (SEG).seg_stp=RT_SOLTAB_NULL |
| #define | RHC_TOL .0001 |
Functions | |
| int | rt_rhc_prep (struct soltab *stp, struct rt_db_internal *ip, struct rt_i *rtip) |
| void | rt_rhc_print (register const struct soltab *stp) |
| int | rt_rhc_shot (struct soltab *stp, register struct xray *rp, struct application *ap, struct seg *seghead) |
| void | rt_rhc_vshot (struct soltab **stp, struct xray **rp, struct seg *segp, int n, struct application *ap) |
| void | rt_rhc_norm (register struct hit *hitp, struct soltab *stp, register struct xray *rp) |
| void | rt_rhc_curve (register struct curvature *cvp, register struct hit *hitp, struct soltab *stp) |
| void | rt_rhc_uv (struct application *ap, struct soltab *stp, register struct hit *hitp, register struct uvcoord *uvp) |
| void | rt_rhc_free (register struct soltab *stp) |
| int | rt_rhc_class (void) |
| int | rt_rhc_plot (struct bu_list *vhead, struct rt_db_internal *ip, const struct rt_tess_tol *ttol, const struct bn_tol *tol) |
| int | rt_mk_hyperbola (struct rt_pt_node *pts, fastf_t r, fastf_t b, fastf_t c, fastf_t dtol, fastf_t ntol) |
| int | rt_rhc_tess (struct nmgregion **r, struct model *m, struct rt_db_internal *ip, const struct rt_tess_tol *ttol, const struct bn_tol *tol) |
| int | rt_rhc_import (struct rt_db_internal *ip, const struct bu_external *ep, register const fastf_t *mat, const struct db_i *dbip) |
| int | rt_rhc_export (struct bu_external *ep, const struct rt_db_internal *ip, double local2mm, const struct db_i *dbip) |
| int | rt_rhc_import5 (struct rt_db_internal *ip, const struct bu_external *ep, register const fastf_t *mat, const struct db_i *dbip) |
| int | rt_rhc_export5 (struct bu_external *ep, const struct rt_db_internal *ip, double local2mm, const struct db_i *dbip) |
| int | rt_rhc_describe (struct bu_vls *str, const struct rt_db_internal *ip, int verbose, double mm2local) |
| void | rt_rhc_ifree (struct rt_db_internal *ip) |
Variables | |
| const struct bu_structparse | rt_rhc_parse [] |
Algorithm -
Given V, H, R, and B, there is a set of points on this rhc
{ (x,y,z) | (x,y,z) is on rhc }
Through a series of Affine Transformations, this set of points will be transformed into a set of points on an rhc located at the origin with a rectangular halfwidth R of 1 along the Y axis, a height H of +1 along the -X axis, a distance B of 1 along the -Z axis between the vertex V and the tip of the hyperbola, and a distance c between the tip of the hyperbola and the vertex of the asymptotic cone.
{ (x',y',z') | (x',y',z') is on rhc at origin }
The transformation from X to X' is accomplished by:
X' = S(R( X - V ))
where R(X) = ( H/(-|H|) ) ( R/( |R|) ) . X ( B/(-|B|) )
and S(X) = ( 1/|H| 0 0 ) ( 0 1/|R| 0 ) . X ( 0 0 1/|B| )
To find the intersection of a line with the surface of the rhc, consider the parametric line L:
L : { P(n) | P + t(n) . D }
Call W the actual point of intersection between L and the rhc. Let W' be the point of intersection between L' and the unit rhc.
L' : { P'(n) | P' + t(n) . D' }
W = invR( invS( W' ) ) + V
Where W' = k D' + P'.
If Dy' and Dz' are both 0, then there is no hit on the rhc; but the end plates need checking. If there is now only 1 hit point, the top plate needs to be checked as well.
Line L' hits the infinitely long canonical rhc at W' when
A * k**2 + B * k + C = 0
where
A = Dz'**2 - Dy'**2 * (1 + 2*c') B = 2 * ((1 + c' + Pz') * Dz' - (1 + 2*c') * Dy' * Py' C = (Pz' + c' + 1)**2 - (1 + 2*c') * Py'**2 - c'**2 b = |Breadth| = 1.0 h = |Height| = 1.0 r = 1.0 c' = c / |Breadth|
The quadratic formula yields k (which is constant):
k = [ -B +/- sqrt( B**2 - 4 * A * C )] / (2 * A)
Now, D' = S( R( D ) ) and P' = S( R( P - V ) )
Substituting,
W = V + invR( invS[ k *( S( R( D ) ) ) + S( R( P - V ) ) ] ) = V + invR( ( k * R( D ) ) + R( P - V ) ) = V + k * D + P - V = k * D + P
Note that ``k'' is constant, and is the same in the formulations for both W and W'.
The hit at ``k'' is a hit on the canonical rhc IFF -1 <= Wx' <= 0 and -1 <= Wz' <= 0.
NORMALS. Given the point W on the surface of the rhc, what is the vector normal to the tangent plane at that point?
Map W onto the unit rhc, ie: W' = S( R( W - V ) ).
Plane on unit rhc at W' has a normal vector N' where
N' = <0, Wy'*(1 + 2*c), -z-c-1>.
The plane transforms back to the tangent plane at W, and this new plane (on the original rhc) has a normal vector of N, viz:
N = inverse[ transpose( inverse[ S o R ] ) ] ( N' )
because if H is perpendicular to plane Q, and matrix M maps from Q to Q', then inverse[ transpose(M) ] (H) is perpendicular to Q'. Here, H and Q are in "prime space" with the unit sphere. [Somehow, the notation here is backwards]. So, the mapping matrix M = inverse( S o R ), because S o R maps from normal space to the unit sphere.
N = inverse[ transpose( inverse[ S o R ] ) ] ( N' ) = inverse[ transpose(invR o invS) ] ( N' ) = inverse[ transpose(invS) o transpose(invR) ] ( N' ) = inverse[ inverse(S) o R ] ( N' ) = invR o S ( N' )
because inverse(R) = transpose(R), so R = transpose( invR ), and S = transpose( S ).
Note that the normal vector produced above will not have unit length.
THE TOP AND END PLATES.
If Dz' == 0, line L' is parallel to the top plate, so there is no hit on the top plate. Otherwise, rays intersect the top plate with k = (0 - Pz')/Dz'. The solution is within the top plate IFF -1 <= Wx' <= 0 and -1 <= Wy' <= 1.
If Dx' == 0, line L' is parallel to the end plates, so there is no hit on the end plates. Otherwise, rays intersect the front plate line L' hits the front plate with k = (0 - Px') / Dx', and and hits the back plate with k = (-1 - Px') / Dx'.
The solution W' is within an end plate IFF
(Wz' + c + 1)**2 - (Wy'**2 * (2*c + 1) >= c**2 and Wz' <= 1.0
The normal for a hit on the top plate is -Bunit. The normal for a hit on the front plate is -Hunit, and the normal for a hit on the back plate is +Hunit.
Authors - Michael J. Markowski
Source - SECAD/VLD Computing Consortium, Bldg 394 The U. S. Army Ballistic Research Laboratory Aberdeen Proving Ground, Maryland 21005-5066
Definition in file g_rhc.c.
|
|
Definition at line 346 of file g_rhc.c. Referenced by rt_rhc_curve(), rt_rhc_norm(), rt_rhc_shot(), and rt_rhc_uv(). |
|
|
Definition at line 347 of file g_rhc.c. Referenced by rt_rhc_curve(), rt_rhc_norm(), rt_rhc_shot(), and rt_rhc_uv(). |
|
|
Definition at line 348 of file g_rhc.c. Referenced by rt_rhc_curve(), rt_rhc_norm(), rt_rhc_shot(), and rt_rhc_uv(). |
|
|
Definition at line 349 of file g_rhc.c. Referenced by rt_rhc_curve(), rt_rhc_norm(), rt_rhc_shot(), and rt_rhc_uv(). |
|
|
|
|
|
Referenced by rt_mk_hyperbola(). |
|
||||||||||||||||
|
|
R T _ R H C _ P R I N T Definition at line 332 of file g_rhc.c. References bn_mat_print(), rhc_specific::rhc_Bunit, rhc_specific::rhc_Hunit, rhc_specific::rhc_invRoS, rhc_specific::rhc_Runit, rhc_specific::rhc_SoR, rhc_specific::rhc_V, and VPRINT. Here is the call graph for this function:  |
|
||||||||||||||||||||
|
R T _ R H C _ S H O T Intersect a ray with a rhc. If an intersection occurs, a struct seg will be acquired and filled in. Returns - 0 MISS >0 HIT Definition at line 363 of file g_rhc.c. References application::a_resource, BU_LIST_INSERT, FAST, seg::l, LOCAL, MAT4X3VEC, NEAR_ZERO, rhc_specific::rhc_cprime, RHC_NORM_BACK, RHC_NORM_BODY, RHC_NORM_FRT, RHC_NORM_TOP, rhc_specific::rhc_SoR, rhc_specific::rhc_V, RT_GET_SEG, RT_HIT_MAGIC, RT_PCOEF_TOL, seg::seg_in, seg::seg_out, seg::seg_stp, SMALL, soltab::st_specific, VJOIN1, VSUB2, X, Y, and Z. |
|
||||||||||||||||||||||||
|
R T _ R H C _ V S H O T Vectorized version. Definition at line 533 of file g_rhc.c. References rt_vstub(). Here is the call graph for this function:  |
|
||||||||||||||||
|
R T _ R H C _ N O R M Given ONE ray distance, return the normal and entry/exit point. Definition at line 549 of file g_rhc.c. References bu_log(), MAT4X3VEC, rhc_specific::rhc_Bunit, rhc_specific::rhc_cprime, rhc_specific::rhc_Hunit, rhc_specific::rhc_invRoS, RHC_NORM_BACK, RHC_NORM_BODY, RHC_NORM_FRT, RHC_NORM_TOP, soltab::st_specific, VJOIN1, VMOVE, VREVERSE, VSET, VUNITIZE, Y, and Z. Here is the call graph for this function:  |
|
||||||||||||||||
|
R T _ R H C _ C U R V E Return the curvature of the rhc. Definition at line 588 of file g_rhc.c. References bn_vec_ortho(), rhc_specific::rhc_b, rhc_specific::rhc_c, rhc_specific::rhc_Hunit, RHC_NORM_BACK, RHC_NORM_BODY, RHC_NORM_FRT, RHC_NORM_TOP, rhc_specific::rhc_rsq, soltab::st_specific, VMOVE, and Y. Here is the call graph for this function:  |
|
||||||||||||||||||||
|
R T _ R H C _ U V For a hit on the surface of an rhc, return the (u,v) coordinates of the hit point, 0 <= u,v <= 1. u = azimuth v = elevation Definition at line 629 of file g_rhc.c. References bn_invpi, FAST, LOCAL, MAT4X3VEC, RHC_NORM_BACK, RHC_NORM_BODY, RHC_NORM_FRT, RHC_NORM_TOP, rhc_specific::rhc_SoR, rhc_specific::rhc_V, soltab::st_specific, VSUB2, X, Y, and Z. |
|
|
R T _ R H C _ F R E E Definition at line 672 of file g_rhc.c. References bu_free(). Here is the call graph for this function:  |
|
|
R T _ R H C _ C L A S S |
|
||||||||||||||||||||
|
R T _ R H C _ P L O T Definition at line 694 of file g_rhc.c. References rt_tess_tol::abs, bn_mat_trn(), bn_pi, BN_VLIST_LINE_DRAW, BN_VLIST_LINE_MOVE, bu_free(), bu_log(), bu_malloc(), ELEMENTS_PER_VECT, rt_db_internal::idb_ptr, LOCAL, MAGNITUDE, MAT4X3VEC, MAT_IDN, NEAR_ZERO, rt_pt_node::next, rt_tess_tol::norm, NULL, rt_pt_node::p, pos, R, rt_tess_tol::rel, rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_ADD_VLIST, RT_CK_DB_INTERNAL, RT_DOT_TOL, RT_LEN_TOL, rt_mk_hyperbola(), rt_ptalloc(), RT_RHC_CK_MAGIC, VADD2, VCROSS, VDOT, VMOVE, VREVERSE, VSET, and VUNITIZE. Here is the call graph for this function:  |
|
||||||||||||||||||||||||
|
R T _ R H C _ T E S S Returns - -1 failure 0 OK. *r points to nmgregion that holds this tessellation. Definition at line 912 of file g_rhc.c. References rt_tess_tol::abs, BN_CK_TOL, bn_mat_trn(), bn_pi, bu_calloc(), bu_free(), BU_LIST_FIRST, bu_log(), bu_malloc(), rt_db_internal::idb_ptr, LOCAL, MAGNITUDE, MAT4X3VEC, MAT_IDN, NEAR_ZERO, rt_pt_node::next, NMG_CK_MODEL, nmg_mrsv(), rt_tess_tol::norm, NULL, rt_pt_node::p, pos, R, rt_tess_tol::rel, rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_CK_DB_INTERNAL, RT_CK_TESS_TOL, RT_DOT_TOL, RT_LEN_TOL, rt_mk_hyperbola(), rt_ptalloc(), RT_RHC_CK_MAGIC, VADD2, VCROSS, VDOT, VMOVE, VREVERSE, VSET, VUNITIZE, Y, and Z. Here is the call graph for this function: 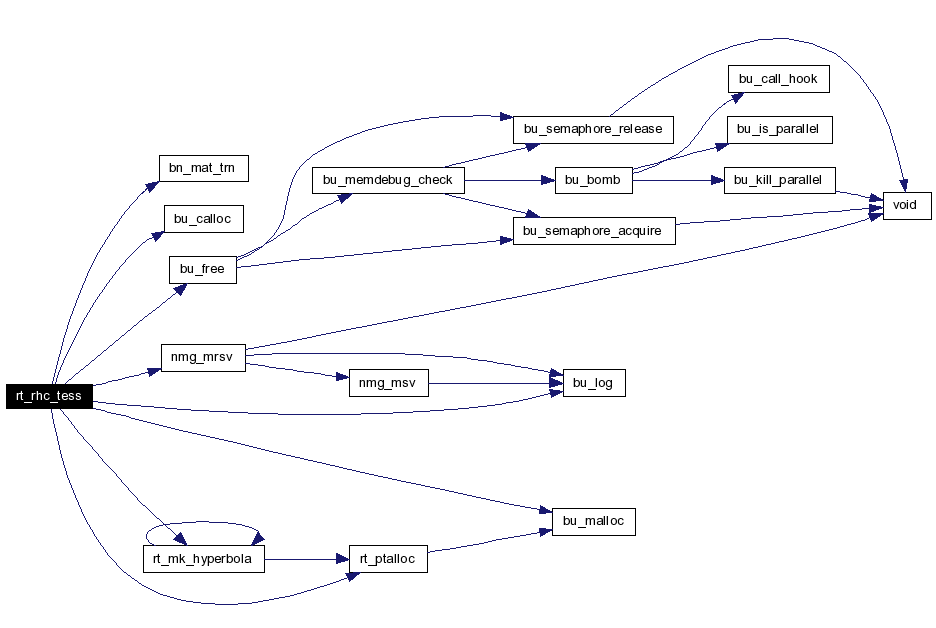 |
|
||||||||||||||||||||
|
R T _ R H C _ I M P O R T Import an RHC from the database format to the internal format. Apply modeling transformations as well. Definition at line 1188 of file g_rhc.c. References BU_CK_EXTERNAL, bu_free(), bu_log(), bu_malloc(), DB5_MAJORTYPE_BRLCAD, bu_external::ext_buf, ID_RHC, ID_SOLID, rt_db_internal::idb_major_type, rt_db_internal::idb_meth, rt_db_internal::idb_ptr, LOCAL, MAT4X3PNT, MAT4X3VEC, rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_magic, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_CK_DB_INTERNAL, RT_RHC_INTERNAL_MAGIC, record::s, record::solidrec::s_values, SMALL_FASTF, and record::u_id. Here is the call graph for this function: 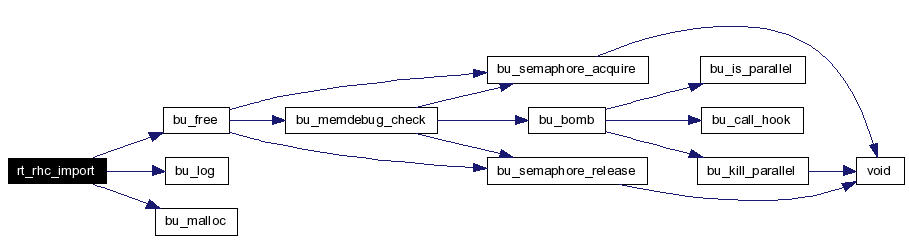 |
|
||||||||||||||||||||
|
R T _ R H C _ E X P O R T The name is added by the caller, in the usual place. Definition at line 1232 of file g_rhc.c. References bu_calloc(), BU_CK_EXTERNAL, bu_log(), bu_external::ext_buf, bu_external::ext_nbytes, ID_RHC, ID_SOLID, rt_db_internal::idb_ptr, MAGNITUDE, NEAR_ZERO, RHC, rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_CK_DB_INTERNAL, RT_DOT_TOL, RT_LEN_TOL, RT_RHC_CK_MAGIC, record::s, record::solidrec::s_id, record::solidrec::s_type, record::solidrec::s_values, VDOT, VMOVE, VSCALE, and VUNITIZE. Here is the call graph for this function: 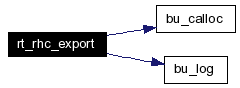 |
|
||||||||||||||||||||
|
R T _ R H C _ I M P O R T 5 Import an RHC from the database format to the internal format. Apply modeling transformations as well. Definition at line 1288 of file g_rhc.c. References BU_ASSERT_LONG, BU_CK_EXTERNAL, bu_free(), bu_log(), bu_malloc(), DB5_MAJORTYPE_BRLCAD, bu_external::ext_buf, bu_external::ext_nbytes, ID_RHC, rt_db_internal::idb_major_type, rt_db_internal::idb_meth, rt_db_internal::idb_ptr, LOCAL, MAT4X3PNT, MAT4X3VEC, ntohd(), rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_magic, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_CK_DB_INTERNAL, RT_RHC_INTERNAL_MAGIC, SIZEOF_NETWORK_DOUBLE, and SMALL_FASTF. Here is the call graph for this function: 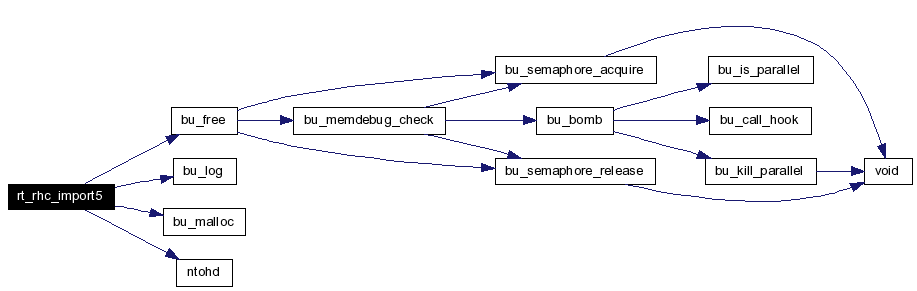 |
|
||||||||||||||||||||
|
R T _ R H C _ E X P O R T 5 The name is added by the caller, in the usual place. Definition at line 1332 of file g_rhc.c. References BU_CK_EXTERNAL, bu_log(), bu_malloc(), bu_external::ext_buf, bu_external::ext_nbytes, htond(), ID_RHC, rt_db_internal::idb_ptr, MAGNITUDE, NEAR_ZERO, rt_rhc_internal::rhc_B, rt_rhc_internal::rhc_c, rt_rhc_internal::rhc_H, rt_rhc_internal::rhc_r, rt_rhc_internal::rhc_V, RT_CK_DB_INTERNAL, RT_DOT_TOL, RT_LEN_TOL, RT_RHC_CK_MAGIC, SIZEOF_NETWORK_DOUBLE, VDOT, VMOVE, VSCALE, and VUNITIZE. Here is the call graph for this function: 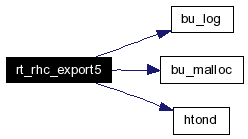 |
|
||||||||||||||||||||
|
R T _ R H C _ D E S C R I B E Make human-readable formatted presentation of this solid. First line describes type of solid. Additional lines are indented one tab, and give parameter values. Definition at line 1388 of file g_rhc.c. References bu_vls_strcat(), rt_db_internal::idb_ptr, INTCLAMP, MAGNITUDE, RT_RHC_CK_MAGIC, X, Y, and Z. Here is the call graph for this function:  |
|
|
R T _ R H C _ I F R E E Free the storage associated with the rt_db_internal version of this solid. Definition at line 1432 of file g_rhc.c. References bu_free(), GENPTR_NULL, rt_db_internal::idb_ptr, rt_rhc_internal::rhc_magic, RT_CK_DB_INTERNAL, and RT_RHC_CK_MAGIC. Here is the call graph for this function: 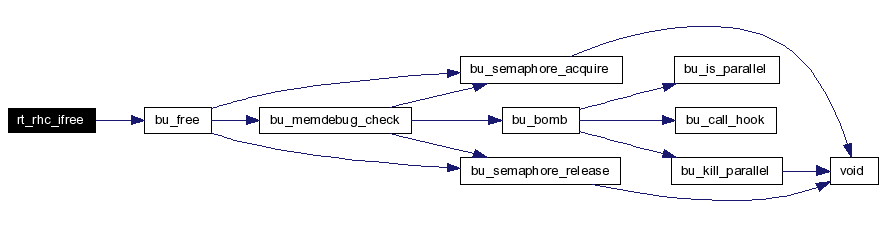 |
|
|
Initial value: {
{ "%f", 3, "V", bu_offsetof(struct rt_rhc_internal, rhc_V[X]), BU_STRUCTPARSE_FUNC_NULL },
{ "%f", 3, "H", bu_offsetof(struct rt_rhc_internal, rhc_H[X]), BU_STRUCTPARSE_FUNC_NULL },
{ "%f", 3, "B", bu_offsetof(struct rt_rhc_internal, rhc_B[X]), BU_STRUCTPARSE_FUNC_NULL },
{ "%f", 1, "r", bu_offsetof(struct rt_rhc_internal, rhc_r), BU_STRUCTPARSE_FUNC_NULL },
{ "%f", 1, "c", bu_offsetof(struct rt_rhc_internal, rhc_c), BU_STRUCTPARSE_FUNC_NULL },
{ {'\0','\0','\0','\0'}, 0, (char *)NULL, 0, BU_STRUCTPARSE_FUNC_NULL }
}
|
 1.4.6
1.4.6