qmath.c File Reference

Quaternion math routines. More...

#include "common.h"
#include <stdio.h>
#include <math.h>
#include "machine.h"
#include "bu.h"
#include "vmath.h"
#include "bn.h"

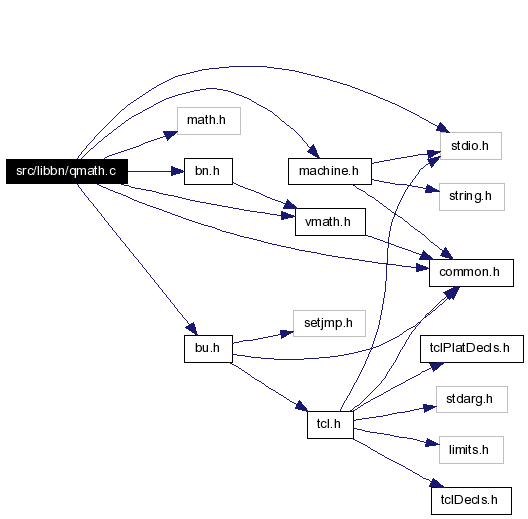
Include dependency graph for qmath.c:

Go to the source code of this file.

Defines
#define	PI   3.14159265358979323264
#define	RTODEG   (180.0/PI)
#define	XX   0
#define	YY   5
#define	ZZ   10
#define	MMM(a, b)   mat[4*(a)+(b)]
Functions
void	quat_mat2quat (register fastf_t *quat, register const fastf_t *mat)
	Convert Matrix to Quaternion.
void	quat_quat2mat (register fastf_t *mat, register const fastf_t *quat)
	Convert Quaternion to Matrix.
double	quat_distance (const fastf_t *q1, const fastf_t *q2)
	Gives the euclidean distance between two quaternions.
void	quat_double (fastf_t *qout, const fastf_t *q1, const fastf_t *q2)
	Gives the quaternion point representing twice the rotation from q1 to q2. Needed for patching Bezier curves together. A rather poor name admittedly.
void	quat_bisect (fastf_t *qout, const fastf_t *q1, const fastf_t *q2)
	Gives the bisector of quaternions q1 and q2. (Could be done with quat_slerp and factor 0.5) [I believe they must be unit quaternions this to work].
void	quat_slerp (fastf_t *qout, const fastf_t *q1, const fastf_t *q2, double f)
	Do Spherical Linear Interpolation between two unit quaternions by the given factor.
void	quat_sberp (fastf_t *qout, const fastf_t *q1, const fastf_t *qa, const fastf_t *qb, const fastf_t *q2, double f)
	Spherical Bezier Interpolate between four quaternions by amount f. These are intended to be used as start and stop quaternions along with two control quaternions chosen to match spline segments with first order continuity.
void	quat_make_nearest (fastf_t *q1, const fastf_t *q2)
	Set the quaternion q1 to the quaternion which yields the smallest rotation from q2 (of the two versions of q1 which produce the same orientation).
void	quat_print (const char *title, const fastf_t *quat)
void	quat_exp (fastf_t *out, const fastf_t *in)
	Exponentiate a quaternion, assuming that the scalar part is 0. Code by Ken Shoemake.
void	quat_log (fastf_t *out, const fastf_t *in)
	Take the natural logarithm of a unit quaternion. Code by Ken Shoemake.

---

Detailed Description

Quaternion math routines.

Unit Quaternions: Q = [ r, a ] where r = cos(theta/2) = rotation amount |a| = sin(theta/2) = rotation axis

If a = 0 we have the reals; if one coord is zero we have complex numbers (2D rotations).

[r,a][s,b] = [rs - a.b, rb + sa + axb]

-1 [r,a] = (r - a) / (r^2 + a.a)

Powers of quaternions yield incremental rotations, e.g. Q^3 is rotated three times as far as Q.

Some operations on quaternions: -1 [0,P'] = Q [0,P]Q Rotate a point P by quaternion Q -1 a slerp(Q,R,a) = Q(Q R) Spherical linear interp: 0 < a < 1

bisect(P,Q) = (P + Q) / |P + Q| Great circle bisector

Author:

Phil Dykstra, 25 Sep 1985

Additions inspired by "Quaternion Calculus For Animation" by Ken Shoemake, SIGGRAPH '89 course notes for "Math for SIGGRAPH", May 1989.

Source -

SECAD/VLD Computing Consortium, Bldg 394
The U. S. Army Ballistic Research Laboratory
Aberdeen Proving Ground, Maryland 21005-5066

Definition in file qmath.c.

---

Define Documentation

#define XX   0

Referenced by quat_mat2quat().

#define YY   5

Referenced by quat_mat2quat().

#define ZZ   10

Referenced by quat_mat2quat().

#define MMM (  a, b   )     mat[4*(a)+(b)]

Referenced by quat_mat2quat().

---