#include "common.h"
#include <stdio.h>
#include <math.h>
#include <strings.h>
#include "machine.h"
#include "bu.h"
#include "vmath.h"
#include "bn.h"
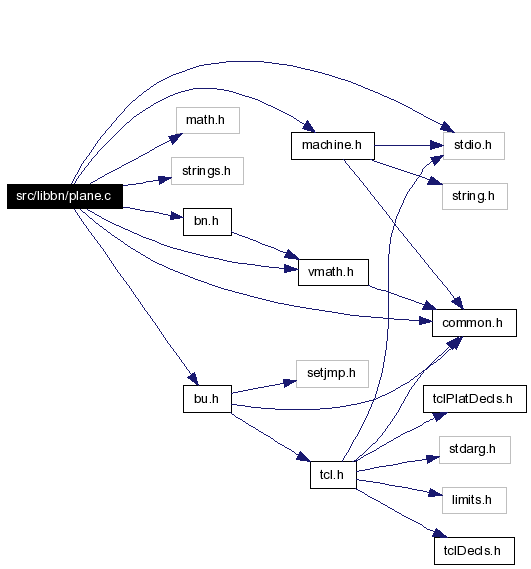
Include dependency graph for plane.c:

Go to the source code of this file.
Defines | |
| #define | UNIT_SQ_TOL 1.0e-13 |
| #define | DETERMINANT_TOL 1.0e-14 |
| #define | ROT_VERT(a, b, c) |
| #define | CHECK_PT(x, y, z) |
Functions | |
| double | bn_dist_pt3_pt3 (const fastf_t *a, const fastf_t *b) |
| Returns distance between two points. | |
| int | bn_pt3_pt3_equal (const fastf_t *a, const fastf_t *b, const struct bn_tol *tol) |
| int | bn_pt2_pt2_equal (const fastf_t *a, const fastf_t *b, const struct bn_tol *tol) |
| int | bn_3pts_collinear (fastf_t *a, fastf_t *b, fastf_t *c, const struct bn_tol *tol) |
| Check to see if three points are collinear. | |
| int | bn_3pts_distinct (const fastf_t *a, const fastf_t *b, const fastf_t *c, const struct bn_tol *tol) |
| int | bn_mk_plane_3pts (fastf_t *plane, const fastf_t *a, const fastf_t *b, const fastf_t *c, const struct bn_tol *tol) |
| int | bn_mkpoint_3planes (fastf_t *pt, const fastf_t *a, const fastf_t *b, const fastf_t *c) |
| Given the description of three planes, compute the point of intersection, if any. | |
| int | bn_2line3_colinear (const fastf_t *p1, const fastf_t *d1, const fastf_t *p2, const fastf_t *d2, double range, const struct bn_tol *tol) |
| Returns non-zero if the 3 lines are colinear to within tol->dist over the given distance range. | |
| int | bn_isect_line3_plane (fastf_t *dist, const fastf_t *pt, const fastf_t *dir, const fastf_t *plane, const struct bn_tol *tol) |
| int | bn_isect_2planes (fastf_t *pt, fastf_t *dir, const fastf_t *a, const fastf_t *b, const fastf_t *rpp_min, const struct bn_tol *tol) |
| Given two planes, find the line of intersection between them, if one exists. The line of intersection is returned in parametric line (point & direction vector) form. | |
| int | bn_isect_line2_line2 (fastf_t *dist, const fastf_t *p, const fastf_t *d, const fastf_t *a, const fastf_t *c, const struct bn_tol *tol) |
| int | bn_isect_line2_lseg2 (fastf_t *dist, const fastf_t *p, const fastf_t *d, const fastf_t *a, const fastf_t *c, const struct bn_tol *tol) |
| Intersect a line in parametric form:. | |
| int | bn_isect_lseg2_lseg2 (fastf_t *dist, const fastf_t *p, const fastf_t *pdir, const fastf_t *q, const fastf_t *qdir, const struct bn_tol *tol) |
| Intersect two 2D line segments, defined by two points and two vectors. The vectors are unlikely to be unit length. | |
| int | bn_isect_lseg3_lseg3 (fastf_t *dist, const fastf_t *p, const fastf_t *pdir, const fastf_t *q, const fastf_t *qdir, const struct bn_tol *tol) |
| Intersect two 3D line segments, defined by two points and two vectors. The vectors are unlikely to be unit length. | |
| int | bn_isect_line3_line3 (fastf_t *t, fastf_t *u, const fastf_t *p, const fastf_t *d, const fastf_t *a, const fastf_t *c, const struct bn_tol *tol) |
| int | bn_isect_line_lseg (fastf_t *t, const fastf_t *p, const fastf_t *d, const fastf_t *a, const fastf_t *b, const struct bn_tol *tol) |
| Intersect a line in parametric form:. | |
| double | bn_dist_line3_pt3 (const fastf_t *pt, const fastf_t *dir, const fastf_t *a) |
| Given a parametric line defined by PT + t * DIR and a point A, return the closest distance between the line and the point. | |
| double | bn_distsq_line3_pt3 (const fastf_t *pt, const fastf_t *dir, const fastf_t *a) |
| double | bn_dist_line_origin (const fastf_t *pt, const fastf_t *dir) |
| Given a parametric line defined by PT + t * DIR, return the closest distance between the line and the origin. | |
| double | bn_dist_line2_point2 (const fastf_t *pt, const fastf_t *dir, const fastf_t *a) |
| Given a parametric line defined by PT + t * DIR and a point A, return the closest distance between the line and the point. | |
| double | bn_distsq_line2_point2 (const fastf_t *pt, const fastf_t *dir, const fastf_t *a) |
| Given a parametric line defined by PT + t * DIR and a point A, return the closest distance between the line and the point, squared. | |
| double | bn_area_of_triangle (register const fastf_t *a, register const fastf_t *b, register const fastf_t *c) |
| Returns the area of a triangle. Algorithm by Jon Leech 3/24/89. | |
| int | bn_isect_pt_lseg (fastf_t *dist, const fastf_t *a, const fastf_t *b, const fastf_t *p, const struct bn_tol *tol) |
| Intersect a point P with the line segment defined by two distinct points A and B. | |
| int | bn_isect_pt2_lseg2 (fastf_t *dist, const fastf_t *a, const fastf_t *b, const fastf_t *p, const struct bn_tol *tol) |
| Intersect a point P with the line segment defined by two distinct points A and B. | |
| int | bn_dist_pt3_lseg3 (fastf_t *dist, fastf_t *pca, const fastf_t *a, const fastf_t *b, const fastf_t *p, const struct bn_tol *tol) |
| Find the distance from a point P to a line segment described by the two endpoints A and B, and the point of closest approach (PCA). | |
| int | bn_dist_pt2_lseg2 (fastf_t *dist_sq, fastf_t *pca, const fastf_t *a, const fastf_t *b, const fastf_t *p, const struct bn_tol *tol) |
| Find the distance from a point P to a line segment described by the two endpoints A and B, and the point of closest approach (PCA). | |
| void | bn_rotate_bbox (fastf_t *omin, fastf_t *omax, const fastf_t *mat, const fastf_t *imin, const fastf_t *imax) |
| Transform a bounding box (RPP) by the given 4x4 matrix. There are 8 corners to the bounding RPP. Each one needs to be transformed and min/max'ed. This is not minimal, but does fully contain any internal object, using an axis-aligned RPP. | |
| void | bn_rotate_plane (fastf_t *oplane, const fastf_t *mat, const fastf_t *iplane) |
| Transform a plane equation by the given 4x4 matrix. | |
| int | bn_coplanar (const fastf_t *a, const fastf_t *b, const struct bn_tol *tol) |
| Test if two planes are identical. If so, their dot products will be either +1 or -1, with the distance from the origin equal in magnitude. | |
| double | bn_angle_measure (fastf_t *vec, const fastf_t *x_dir, const fastf_t *y_dir) |
| double | bn_dist_pt3_along_line3 (const fastf_t *p, const fastf_t *d, const fastf_t *x) |
| Return the parametric distance t of a point X along a line defined as a ray, i.e. solve X = P + t * D. If the point X does not lie on the line, then t is the distance of the perpendicular projection of point X onto the line. | |
| double | bn_dist_pt2_along_line2 (const fastf_t *p, const fastf_t *d, const fastf_t *x) |
| Return the parametric distance t of a point X along a line defined as a ray, i.e. solve X = P + t * D. If the point X does not lie on the line, then t is the distance of the perpendicular projection of point X onto the line. | |
| int | bn_between (double left, double mid, double right, const struct bn_tol *tol) |
| int | bn_does_ray_isect_tri (const point_t pt, const vect_t dir, const point_t V, const point_t A, const point_t B, point_t inter) |
| int | bn_hlf_class (const fastf_t *half_eqn, const fastf_t *min, const fastf_t *max, const struct bn_tol *tol) |
| Classify a halfspace, specified by its plane equation, against a bounding RPP. | |
| int | bn_distsq_line3_line3 (fastf_t *dist, fastf_t *P, fastf_t *d_in, fastf_t *Q, fastf_t *e_in, fastf_t *pt1, fastf_t *pt2) |
| Calculate the square of the distance of closest approach for two lines. | |
| int | bn_isect_planes (fastf_t *pt, const fastf_t(*planes)[4], const int pl_count) |
| Calculates the point that is the minimum distance from all the planes in the "planes" array. If the planes intersect at a single point, that point is the solution. | |
| int | bn_isect_lseg_rpp (fastf_t *a, fastf_t *b, register fastf_t *min, register fastf_t *max) |
| Intersect a line segment with a rectangular parallelpiped (RPP) that has faces parallel to the coordinate planes (a clipping RPP). The RPP is defined by a minimum point and a maximum point. This is a very close relative to rt_in_rpp() from librt/shoot.c. | |
Definition in file plane.c.
|
|
Referenced by bn_isect_line2_line2(), and bn_isect_line3_line3(). |
|
|
Value: Referenced by bn_rotate_bbox(). |
|
|
Value: d = (x)*half_eqn[0] + (y)*half_eqn[1] + (z)*half_eqn[2] - half_eqn[3];\ if( d < -tol->dist ) { \ if( class == BN_CLASSIFY_OUTSIDE ) \ return BN_CLASSIFY_OVERLAPPING; \ else class = BN_CLASSIFY_INSIDE; \ } else if( d > tol->dist ) { \ if( class == BN_CLASSIFY_INSIDE ) \ return BN_CLASSIFY_OVERLAPPING; \ else class = BN_CLASSIFY_OUTSIDE; \ } else return BN_CLASSIFY_OVERLAPPING Referenced by bn_hlf_class(). |
 1.4.6
1.4.6