Difference between revisions of "User:Phoenix/GSoc2013/Reports"
From BRL-CAD
(→Week 5) |
(→Week 5) |
||
| Line 147: | Line 147: | ||
*** If we assume the two surfaces are C-infinity, we can use the theorem 3 in paper http://libgen.org/scimag1/10.1016/S0010-4485%252896%252900099-1.pdf (Thanks to Bryan Bishop). This can be reduced to several curve-surface overlap problems (already implemented) because the overlap region is bounded by surface boundaries. | *** If we assume the two surfaces are C-infinity, we can use the theorem 3 in paper http://libgen.org/scimag1/10.1016/S0010-4485%252896%252900099-1.pdf (Thanks to Bryan Bishop). This can be reduced to several curve-surface overlap problems (already implemented) because the overlap region is bounded by surface boundaries. | ||
*** Otherwise, we need to get points inside the overlap region (using surfA->NormalAt(u,v) and surfB->NormalAt(s,t)), and then find the boundary (merge the triangles using the points as vertexes). These approach doesn't require continuity, but is very slow (too many bounding boxes and intersection points) and may lack accuracy (we may not have points on the boundaries) | *** Otherwise, we need to get points inside the overlap region (using surfA->NormalAt(u,v) and surfB->NormalAt(s,t)), and then find the boundary (merge the triangles using the points as vertexes). These approach doesn't require continuity, but is very slow (too many bounding boxes and intersection points) and may lack accuracy (we may not have points on the boundaries) | ||
| + | * July 17 | ||
| + | ** Some slight modifications to SSI (Commit 56091) | ||
| + | ** Solved the under-determined system with Newton iterations using pseudo-inverse. (ON_Matrix::Invert()) can do this) | ||
| + | ** Began working on overlaps: | ||
| + | *** Bezier patches satisfy the theorem 3 mentioned above. Since the Bezier patches for a NURBS surface are always bounded at the knots, we actually don't need to generate the Bezier patches explicitly, and we can get the boundaries of them using IsoCurve() on knots. | ||
| + | *** Get the 3D overlap boundary segments. (2D is working in process because CSI doesn't report a 2D curve on the surface) | ||
| + | *** Some tests and bug fixing. | ||
= Test Results = | = Test Results = | ||
Revision as of 06:31, 17 July 2013
Contents
Log
Community bonding
- May 28
- Create the log page
- Things have done:
- Test program for SSI and a test geometry file
- Some improvement with SSI and API design
- June 3
- As I will have my final exams during the first week that coding begins, so I'd like to move some work ahead.
- Begin to add P/P, P/C and P/S support. Implement ON_PX_EVENT for reporting the intersections.
- TODO: Implement P/C, P/S and ON_PX_EVENT::IsValid().
- June 4
- Eliminate max_dis in the brep command for SSI.
- Extended the brep command to handle P/P, P/C, P/S, C/C and C/S.
- Modified the wiki page of the brep command.
- Fix the format of ON_PX_EVENT::Dump(). (Add "\n")
- June 7
- Try to add PS support using get_closest_point().
- Test the functionality of the PS function - it seems that there's a problem when try (0,0,5) on a sphere of radius 5 and centered at the origin (it should be an intersect, but get_closest_point() returns (0,0,-5) resulting in no intersections).
- June 12
- Calculate point-curve intersection using sub-division.
- Do some simple testing on PCI. It works.
Week 1
- June 17
- Coding period begins!
- Put the tolerance into consideration in the IsPointIn() test in PCI.
- Write a test program on sphere to test P/P, P/C and P/S.
It seems that get_closest_point() is not always robust. :( Maybe it's not a good choice for P/S.
- June 18
- Use macros to represent default tolerance and change it to 0.001 (the same as the default tolerance of curve/curve, curve/surface, surface/surface defined by openNURBS)
- Consider the input u_domain and v_domain for the result of point-surface intersection.
- June 19
- Busy with the course projects and preparing a final exam. Didn't have much time for BRL-CAD.
- June 20
- Found the problem causing get_closest_point() to fail
- get_closest_point() sometimes give us the 'farthest' point.
- => getClosestPointEstimate() didn't work.
- => The surface tree are not built correctly.
- => It seems that we inappropriately prepTrims when m_removeTrimmed is false, causing get_closest_point() to fail. Someone who wrote this code needs to check whether this change is correct.
- Use a smaller depth for PSI to improve performance.
- Found the problem causing get_closest_point() to fail
- June 21
- Added Newton-Raphson iteration in PCI to improve accuracy (using the one from subdivision and linear approximation as a starting point)
- After test, it can work with tolerance set to ON_ZERO_TOLERANCE!
- Added Newton-Raphson iteration in PCI to improve accuracy (using the one from subdivision and linear approximation as a starting point)
Week 2
- June 24
- The plane was delayed for a long time. It took almost the whole day to get to Beijing. :(
- Set removeTrimmed to false, otherwise the surface tree cannot be built correctly - since the last change raised a raytrace problem.
- June 25
- Began to implement curve-curve intersections.
- First using sub-division to find the intersecting bounding boxes.
- Then use Newton-Raphson iterations to get an accurate result.
- Finally check the validity of the solutions and check overlap.
- More tests and improvements are needed.
- Added the new CCI and CSI functions to brep_debug.cpp.
- Began to implement curve-curve intersections.
- June 26
- Improvements and bug fixing of curve-curve intersection
- Add tolerance value in the bounding box intersections.
- Check duplication before appending to the array x.
- In the Newton-Raphson iterations, if the inverse fails, we try another two directions.
- More work on the tolerance value to get a more accurate and correct result.
- Add a test program for curve-curve intersections.
- Improvements and bug fixing of curve-curve intersection
- June 27
- Continued improving curve-curve intersection
- Merge the overlap events that are continuous.
- Eliminate the intersection points that are inside the overlap events.
- Some special handling for linear curves.
- Add another test for overlaps.
- Continued improving curve-curve intersection
- June 28
- More work on CCI
- Assign values to m_a[1], m_A[1], etc. even if it's ccx_point event (according to openNURBS declarations in other/openNURBS/opennurbs_x.h)
- Fixed the wrong curve used in detecting overlaps.
- Added more comments to document the intersection approaches.
- Studied materials on curve-surface intersections and ready to get started.
- More work on CCI
Week 3
- July 1
- Began to implement curve-surface intersections
- Use sub-division and Newton-Raphson iterations.
- It's similar to curve-curve intersections.
- Began to implement curve-surface intersections
- July 2
- Added tests for curve-surface intersections.
- Improved curve-surface intersections
- Check the endpoints of the line segment when computing its intersection with a boundary plane.
- Consider NaN.
- Add fabs() when calculating the line_t.
- Fixed a typo in brep.c ("CS" for curve-surface rather than "PC").
- July 3
- Added another test for CSI (line & torus).
- Continued improving curve-surface intersections.
- Reused surface tree - avoid generating the surface tree again and again.
- Added some special splitting machanism for polylines.
- Comparing doubles cannot use minus directly.
- If the starting point is good enough, we don't need Newton iterations.
- When merging, m_b should be consistent with m_a.
- Values of 3D and 2D spaces should have different tolerances. And consider the 2D tolerance when merging.
- July 4
- Started to work on surface-surface intersections (TDD)
- Did some clean up to the original code.
- Split the two steps (intersecting bounding boxes and triangular approximation).
- Dealt with single points, and checked validity of the solutions.
- Using tests (csgbrep.g): brep sph.brep intersect tor.brep 0 0
- Started to work on surface-surface intersections (TDD)
- July 5
- Improve SSI
- Dealt with surface boundaries (using CSI).
- Some special handling for closed surfaces - added function closed_domain().
- Eliminated duplicated points using a naive approach.
- Improve SSI
Week 4
- July 8
- Continued SSI
- Fixed bugs of triangle intersections - wrong line_normal for B, floating point issues (== is not sufficient), coincident planes cases, and calculate the barycentric coordination with ON_Solve2x2() in case that the inversion fails.
- Calculate max_dis using the length of bounding box diagonal, in case that both volumes are zero.
- Modified brep_debug.cpp and test_ssi.cpp to deal with intersection points (use spheres to represent the points).
- Continued SSI
- July 9
- Uploaded some test images to this log with arb_intersect.g and csgbrep.g
- Use 2D intersection tolerance with the 2D distances.
- Linear fitting with the 2D intersection curves.
- July 10
- Perform Newton iterations to get more accurate surface-surface intersection points. (newton_ssi() in intersect.cpp)
- Fixed a bug in triangle intersections raised by points_on_line.
- More elegant SSI result display.
- Did more tests and uploaded result images. (A problem comes out with the tests, as described below)
- July 11
- Worked on fitting the curves that SSI generates.
- Used an independent function to work on curve fitting.
- Added more fitting machanisms.
- Arc fitting - use ON_Curve::IsArc(). But tests seems that it cannot work well. I'll figure out why this happens.
- Ellipse fitting - ON_Curve::IsEllipse() cannot work because it only calls IsArc() in it. And it can not figure out when the curve is an elliptical arc. So I first wanted to use least square fitting provided by http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.83.7803, but found that openNURBS provided us with ON_GetConicEquationThrough6Points() and ON_IsConicEquationAnEllipse() which are very useful and decided to use them. The code works well, and these functions are also very helpful in other conic fittings (hyperbola, parabola).
- Worked on fitting the curves that SSI generates.
- July 12
- Fixed a bug of fitting
- The original code cannot deal with elliptical arcs that cross the point where t=0 - Duplicate the ellipse curve to make its domain [0, 4*pi].
- Tests and fixing the SSI code.
- Use a plane and an elliptic parabolic surface (epa). See the images below.
- Use max_dis_u (v, s, t) seperately as the scale of their domains may differ a lot. Before this, the result is totally a mess, but after this it's much better.
- Eliminate unnecessary collinear points on the polyline curves.
- Remove the arc fitting code, because ON_PolylineCurve::IsArc() always returns false. The elliptical arc fitting code below will work for this.
- Fixed a bug of fitting
Week 5
- July 15
- Normalized the intersection curves (use domain [0, 1]), and checked tangent events.
- Checked domain parameters passed to ON_Intersect().
- Used seaming curves to handle intersecting intersection curves.
- If two curves have points whose distance is less than max_dis (also consider the 2D distances), and they originally don't intersect (use curve-curve intersections), we generated a seaming curve to 'link' them together. Sometimes the seaming curves can be merged if they are continuous to one of the old curves.
- July 16
- Read papers to get ideas to handle overlaps in surface-surface intersections.
- Discusses with other developers on the mailing list.
- Two approaches come to mind:
- If we assume the two surfaces are C-infinity, we can use the theorem 3 in paper http://libgen.org/scimag1/10.1016/S0010-4485%252896%252900099-1.pdf (Thanks to Bryan Bishop). This can be reduced to several curve-surface overlap problems (already implemented) because the overlap region is bounded by surface boundaries.
- Otherwise, we need to get points inside the overlap region (using surfA->NormalAt(u,v) and surfB->NormalAt(s,t)), and then find the boundary (merge the triangles using the points as vertexes). These approach doesn't require continuity, but is very slow (too many bounding boxes and intersection points) and may lack accuracy (we may not have points on the boundaries)
- July 17
- Some slight modifications to SSI (Commit 56091)
- Solved the under-determined system with Newton iterations using pseudo-inverse. (ON_Matrix::Invert()) can do this)
- Began working on overlaps:
- Bezier patches satisfy the theorem 3 mentioned above. Since the Bezier patches for a NURBS surface are always bounded at the knots, we actually don't need to generate the Bezier patches explicitly, and we can get the boundaries of them using IsoCurve() on knots.
- Get the 3D overlap boundary segments. (2D is working in process because CSI doesn't report a 2D curve on the surface)
- Some tests and bug fixing.
Test Results
- src/librt/tests/arb_intersect.g
- csgbrep.g
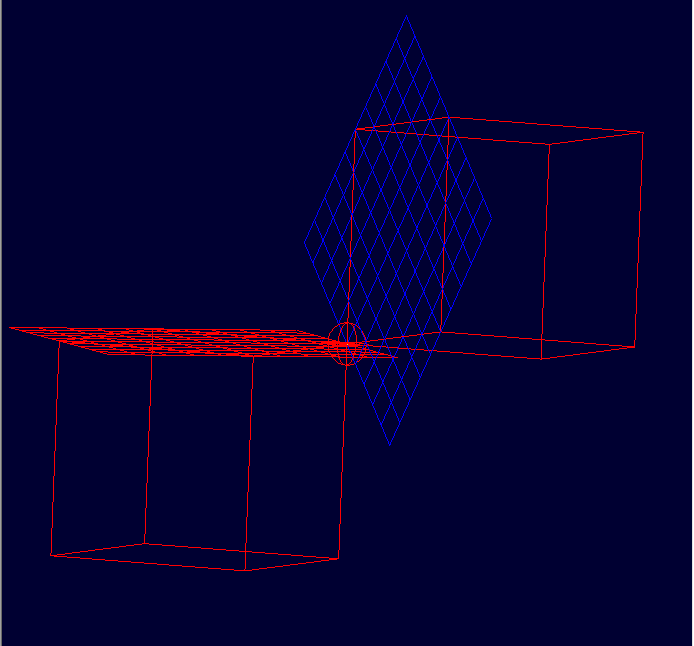
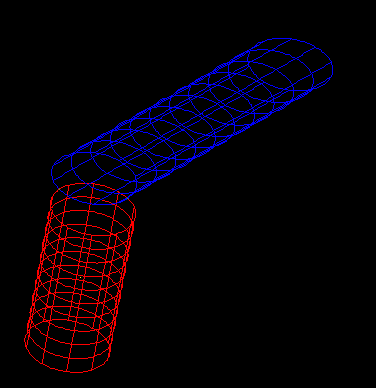
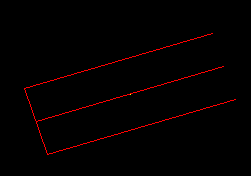
- Intersection of two rcc's (They both have a bottom face that overlaps with each other, and the intersection curve of their side faces is a circle displayed in green.)
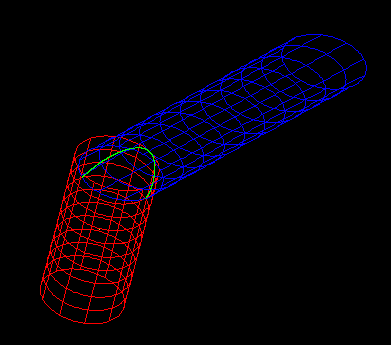
- We translate and rotate the blue rcc, and intersect again its side face with the red one's side face, and get a 3D intersection curve. (Displayed in green)
- This time, their bottom are in the same plane, but only partly overlapped. The intersection of their side faces should be two points (If you look at the image below carefully, you can see a green point in the intersection).
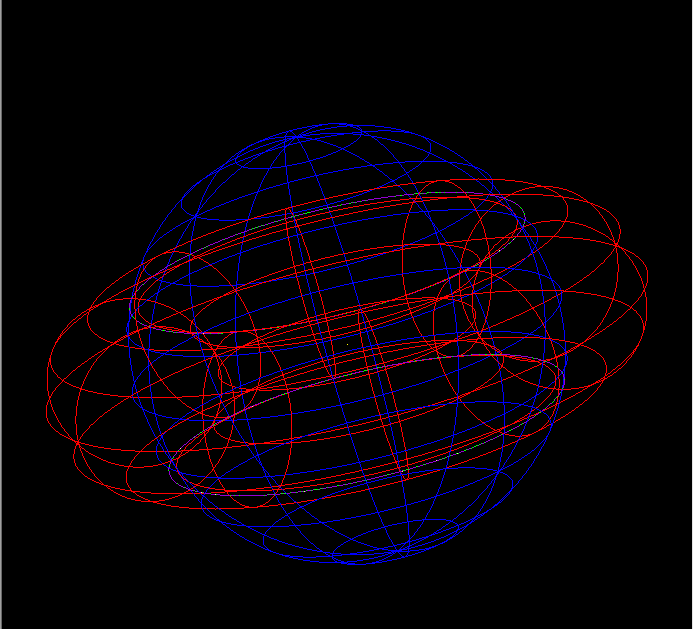
- The below intersection has been described in paper http://www.sciencedirect.com/science/article/pii/0010448596000139. At a glance, the intersections look perfect (The left are 3D intersections and the right are 2D parametric ones.) But if you zoom the view, you can see some difference (The third image)
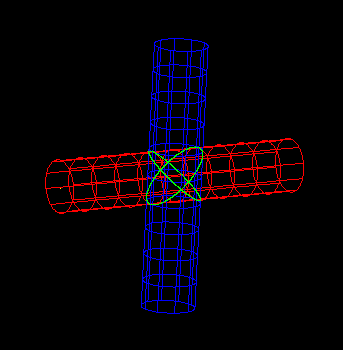
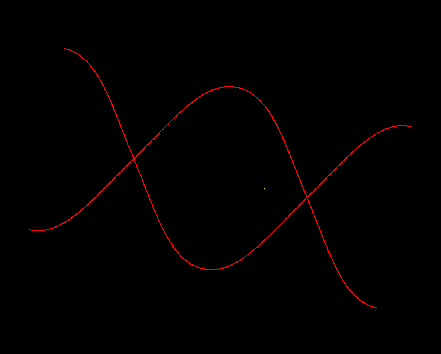

- This problem raised because the two intersection curves intersect with each other, but according to our fitting mechanism, one intersection point can only belong to ONE curve, and points can not be duplicated. So you can see that the two curves are actually separated when zoomed. How to solve this problem? I'm still struggling to find a solution. Hope anyone who see this log can share your ideas. :)
- Some work on July 15 (using seaming segments) is to solve this problem.
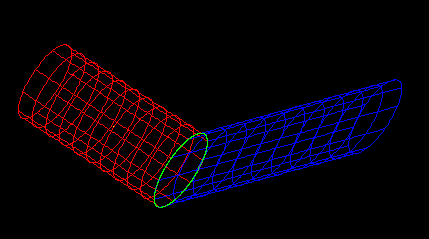
- An elliptic parabolic surface (epa side face) and a plane.
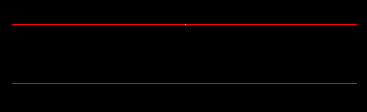
- The left image is the result before we use separate max_dis_u (v, s and t). The right image is the result after we fix this. The problem raises because the domain of the two parameters differ a lot (one is [0, 6.28] and the other is [0, 2000]). For example, two points (0, 0) and (6.28, 1) should not be neighbors, of course, but in the global scale majorly determined by the large domain [0, 2000], they become neighbors and the result is totally messy.

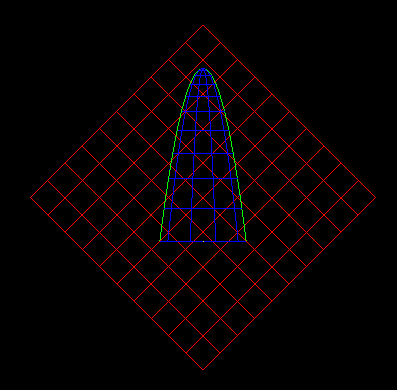
- The below are 2D parametric curves. The left is the projection on the plane surface (it's a parabola) and the right is the projection on the parabolic surface (it's some line segments).

Original development timeline
- - June 17 (~4 weeks)
- Study the papers on this topic
- Discuss with other developers
- Some code clean up in the current SSI routine
- Write a test program to test SSI
- June 17 - June 23 (1 week)
- Lower dimension intersections
- P/P, P/C, P/S
- With the support of openNURBS
- Tests and documentations
- Lower dimension intersections
- June 24 - July 7 (2 weeks)
- Intersections regarding curves
- C/C, C/S
- Subdivision - curve trees, surface trees
- Tests and documentations
- Intersections regarding curves
- July 7 - Aug. 4 (4 weeks)
- TDD on SSI
- Test the SSI
- Find the problems
- Fix the bugs
- Find more bugs and fix them
- Degenerated cases
- Try to get the code faster
- Fit the curve to a lower order if possible
- Documentations
- Comment in code
- Write some extra document on SSI (algorithms, problems, TODOs...)
- Mid-term evaluation in July 29 - Aug. 2
- TDD on SSI
- Aug. 5 - Aug. 18 (2 weeks)
- Finish the surface partitioning
- Polygon partitioning
- Curve-curve intersection
- Tests
- Trims may intersect
- Finish the surface partitioning
- Aug. 19 - Aug. 25 (1 week)
- Add connectivity graph support
- Generate connectivity graphs for objects
- Design proper data structures for the graph
- Add connectivity graph support
- Aug. 26 - Sept. 1 (1 week)
- Inside-outside tests
- Curve-surface intersection
- BFS of the graph to determine inside/outside
- Inside-outside tests
- Sept. 2 - Sept. 8 (1 week)
- Generate valid ON_Brep objects
- Read code in IsValid() functions
- Add elements (trim, edge, etc.)
- Try to pass the validation
- Extend the brep command in MGED
- Generate valid ON_Brep objects
- Sept. 9 - Sept. 15
- Robustness Issues
- Deal with the degenerated cases
- All 3 steps should be modified
- Tests
- Fix bugs
- Improve performance
- Robustness Issues
- Sept. 16 - Sept. 22 (1 week)
- Pencils down
- Code clean up
- Documentation (wiki pages)
- Pencils down
- Sept. 23 - Sept. 27 (1 week)
- Final evaluation
- Submit code to Google