Difference between revisions of "Libpg : A parametrics/constraint library"
Homovulgaris (talk | contribs) (→Extensibility) |
|||
| Line 1: | Line 1: | ||
| + | {{DesignDocument}} | ||
| + | |||
= libpg : A parametrics/ constraint library = | = libpg : A parametrics/ constraint library = | ||
Revision as of 10:20, 23 April 2008
libpg : A parametrics/ constraint library
Proposed sytem for parametrics and constraint implementation by Dawn Thomas (homovulgaris)
Provision for Parametrics and constraints greatly improves the performance of a Computer Aided Design System both in terms of geometry generation as well as analysis. Considering the unix model of division into multiple tools and libraries for individual functions as well as the fact that parametric/constraint functionalities are not critical elements in terms of geometry generation and raytracing, a logical solution would be the implemenation of a separate library (libpg)
Function
libpg adds the following provisions to BRL-CAD system
- Creation & Modification of parameter-based geometry objects
- Creation of constraints between geometry objects
- Creation & Storage of Parametric Objects (non-geometric)
- Modification of geometry objects in .g files to indicate parametric nature
Part 1 would include building parametric objects based on existing non-parametric geometry objects as well as generation of purely parametric geometry. libpg acts as a library which sits above librt using the librt methods for creation and modification of geometry
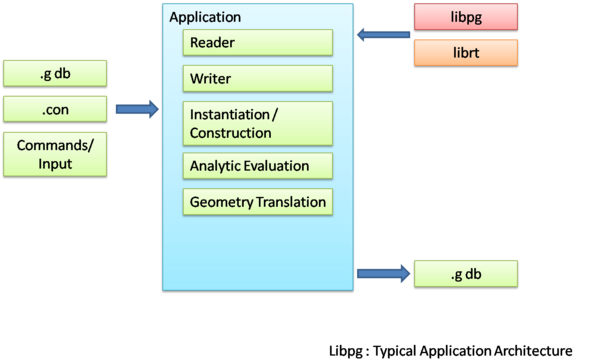
Architecture
The above mentioned functionalities can be clearly expressed as the following capabilities which libpg provides any application
- Input/Output
- Reader
- Writer
- Geometry Translation
- Instantiation/Construction
- Analytic Evaluation
- Numeric Evaluation
Reader and Writer are the respective set of functions which deal with reading and writing information from and onto the .g database constraint files, command input etc. Geometry translation is a primarily a feature for interoperability of libpg package with other CAD geometry systems. Using this method we can follow an independent system of geometry type within libpg if necessary and the Geometry Translation function effectively translates any type of geometry into the libpg standard. libpg standard can be the .g standard of geometry type itself. Using the data thus translated or read from the database , Instantiation and construction of objects is undertaken.
A system of Object overlay is very efficient in the production of parametric geometry objects. Basically for every non-parametric geometry object which is used in the generation of a parametric geometry object we create an equivalent parametric geometric object and use it as an overlay. In this way we will have a comprehensive list of all geometry used in parametrization and would simplify procedure calling.
Once the existing objects are thus instantiated in the cache / display ( which would solve the problem of timestamping in a sense ) equation evaluation is done for generation of new geometry objects. As shown below in the object structure the various details required for the creation of a new parametric object are
- Parent Set
- Parameter Set
Evaluation system is further detailed out below
Object Architecture
An object oriented method of implementation would be the creation of a mixed ( in the sense that they contain both geometric and non-geometric information ) object. The object architecture is as shown below which shows the data types as well as the public and private methods.
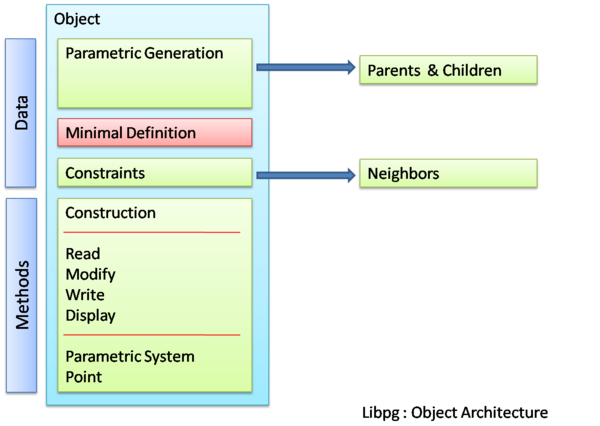
Parametric Geometric Objects
From an Object Oriented point of view the major advantages is in terms of the structuring of data and in particular the system of calling methods or procedures. In effect each object knows how to evaluate equations within its space. For example a line or a curve knows ( has a method to ) calculate and return the coordinates of a point with a certain parameter value in its space ( a point at 0.6 ratio of length of the curve) With this value ( coordinates) thus returned and with the existing knowledge ( parent: curveid , parameter value:0.6 ) a parametric point object has the methods to instantiate it and store it.
Constraint Objects
The above method is efficient and useful only in the generation, modification and analysis of new geometry based on existing parametric/ non-parametric geometry. The evaluation method for constraints between already existing independent geometry would require special constraint objects. The effective difference between these objects and the earlier arises from the fact that generation of the parametric geometric objects depend on parametrics whereas constraints may or may not be feasible and thus evaluation would result in multiple solutions and they represent relationship between two independently defined elements ( parametrically or not )
Evaluation System
It would be ideal to provide both analytical and numeric evaluation methods the second one being of primary importance in terms of constraint based calculations. Considering the standard methods of parametrization ( see Enumeration below ) I think the implementation of an analytic solving system would be easier. Though for the solution of more complex equation as well as majority of constraints , libpg will have to provide support for numerical solutions.
Enumeration of Parameters and Constraints
Various standard methods of parametrics and constraints available in CAD Programs ( CATIA as a case study )
Parametrics
- Point
- Coordinates
- On Curve
- On Plane
- On Surface
- Circle/Sphere Centre
- Tangent on Curve
- Between (2 points)
- Extremum
- Extremum Polar
- Line
- Point-Point
- Point-Direction
- Angle/Normal to the curve
- Tangent to the Curve
- Normal to the surface
- Bisecting
- Plane
- Offset from plane
- Parallel through Point
- Angle/Normal to Plane
- Three points
- Two Lines
- Point and Line
- Planar Curve
- Normal to Curve
- Tangent to Surface
- Equation
- Mean through points
- Axis
- Polyline
- Circle
- Corner
- Connect Curve
- Conic
- Spline
- Helix
- Spiral
Constraints
- Distance
- Length
- Angle
- Radius/Diameter
- Semimajor axis
- Semiminor axis
- Symmetry
- Midpoint
- Equidistant point
- Fix
- Coincidence
- Cocentricity
- Tangency
- Parallelism
- Perpendicular
- Horizontal
- Vertical
- Angle with axis